The Laws of Circuit - you can learn and practice by just reading

copyright. Charles Kim 2006

 

KVL (Kirchhoff's Voltage Law) and Roller Coaster Ride

 

I hate roller coaster. Actually I do not. I hate riding roller coaster. I still do not understand those riding and enjoying folks in the numerous amusement parks. I did ride a roller coaster once and instantly I decided to hate riding one. That's a million years ago, anyway. However, riding roller coaster could help you better understand KVL (Kirchhoff's Voltage Law).

 

KVL first. KVL is about voltage. In other words, the sum of voltages surrounding a loop in a circuit must be zero. The tricky point here is that each voltage in the loop should carry a sign with its value in the algebraic sum equation. In other words, the algebraic sum equation should look like: (+V1)+(+V2)+(-V3)+(-V4)=0 or (+20)+(+2)+(-2)+)+(-20)=0. The question is how do we determine the signs of the voltages. So let's ride a roller coaster, minus me.

 

A roller coaster is not roller coaster if there is no climbing up and climbing down, with very high speed. Actually the ride does not have any flat track span. Otherwise, it would not attract any riders except me. Side bar: Voltage is a potential difference between two points. Higher potential side is marked with plus or positive (+) polarity, and the lower side, minus or negative (-) polarity. The voltage can be a voltage source with given value and polarities in the circle symbol, or a voltage developed across a resistor, or a voltage across a current source. Another side bar: negative power indicates supplied power and positive power consumed power. At least the convention in circuit theory in the U. S.

 

Back to the roller coaster. In the climbing up track span, it needs energy to pull it up to higher position. In the down track span, it consumes the energy gained from the up drive. In the ride, you meet many voltages: voltage source, voltage across a resistor, voltage across another resistor, or voltage across a current source. A voltage must have polarities: + and -. When the roller coaster rides along the loop, it goes in one direction, whether climbing up or dropping down. 

 

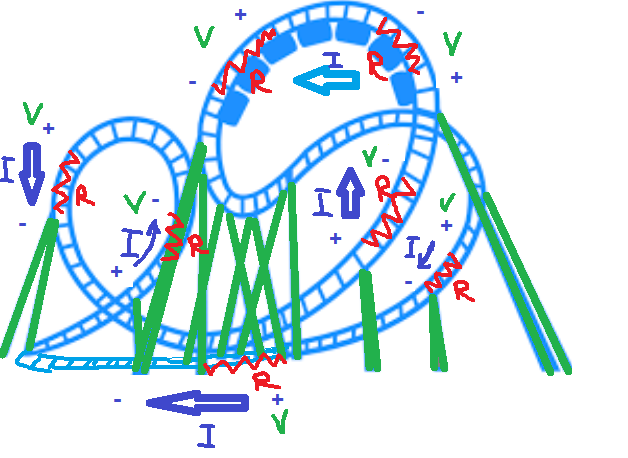In KVL once you choose which direction your roller coaster runs (clockwise or counterclockwise) on the loop, you should not change the direction in the middle of your ride. Never. Butyou can select the direction of your ride before your start.  The direction of the roller coaster can be thought as the current flow direction in a circuit loop.

 

By the way, how and who determines the voltage polarity at the first before applying KVL? You. Basically you do on almost all voltages in the circuit. Except one. Voltage source: independent or dependent. Since voltage sources come with polarity of + and -, you have to honor them. On a resistor, you can first determine the current flow direction and you follow the voltage polarity honoring the passive convention. Or you simply decide your voltage polarity first and let the current flow direction flow according to the passive convention. All right. Now welcome aboard KVL and sit back and relax for a wild ride. And I am watching you up.

WWW.MWFTR.COM